Matematiikka/Murto- ja sekaluvut

Tällä oppitunnilla opetellaan käyttämään murtolukuja. Myös murtoluvuilla laskeminen kerrotaan tällä tunnilla.

Animaatio neljänneksistä.

Murtoluvut

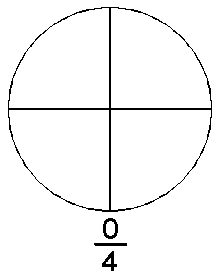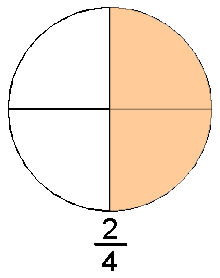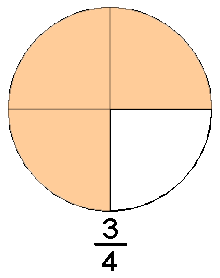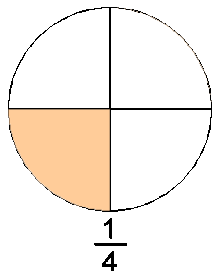
Desimaalilukujen lisäksi murtoluvut voivat olla yhtä pienempiä lukuja. Murtolukuja ovat esimerkiksi ${\frac {1}{2}}$ ja ${\frac {5}{7}}$. Edellä olevat murtoluvut kahdesosa tai kahdennes ja viisi seitsemäsosaa tai viisi seitsemännestä. Murtoluvut koostuvat osoittajasta ja nimittäjästä. Ylempi/etummainen luku on osoittaja ja alimmainnen tai takimmainen on nimittäjä.

${\frac {5}{6}}$ Osoittaja on ylempi luku, eli tässä murtoluvussa luku 5, ja nimittäjä on alempi luku, eli tässä murtoluvussa luku 6.

Nimittäjä on se kuinka monelle yksi on jaettu ja osoittaja kertoo kuinka monta nimittäjää on. Desimaaliluvutkin ovat tavallaan murtolukuja (esim. 0,5 on viisi kymmenesosaa tai kahdesosa). Murtolukuja käytetään kun lukua ei voida ilmoittaa tarkasti desimaalilukuna esimerkiksi 1/3 sillä kymmenen ei ole jaollinen kolmelle. Niitä käytetään myös silloin kun ne ovat selkeämpiä kuin desimaaliluvut.

Sekaluvut

Sekaluvut ovat lukuja jotka ovat arvoltaan yhtä suurempia, mutta eivät kokonaisia. Sekaluvut merkitään $1{\frac {1}{2}}$ (puolitoista). Sekaluvut käyttäytyvät samoin kuin murtoluvut.

Laventaminen

Laventaminen tarkoittaa murtoluvun osoittajan ja nimittäjän kertomista samalla luvulla (paitsi nolla). Luvun arvo ei silti muutu miksikään. Laventamista käytetään kun halutaan saada murtoluvuille sama nimittäjä. Yhteinen nimittäjä löytyy aina kertomalla luvut toisillaan.

Laventava luku merkitään murtoluvun vasempaan yläindeksiin, ja lisätään oikea sulku:

${\frac {^{c)}a}{b}}={\frac {c\cdot a}{c\cdot b}}$

Esimerkki laventamisesta:

${\frac {^{2)}2}{3}}={\frac {2\cdot 2}{2\cdot 3}}={\frac {4}{6}}$

Esimerkiksi murtolukujen yhteen- ja vähennyslaskuissa lavennetaan murtoluvut samannimisiksi laskuoperaation suorittamiseksi:

${\frac {^{2)}2}{3}}+{\frac {1}{6}}={\frac {4}{6}}+{\frac {1}{6}}={\frac {5}{6}}$

Supistaminen

Supistaminen on laventamisen vastakohta eli osoittajan ja nimittäjän jakaminen yhteisellä luvulla. Esimerkiksi ${\frac {2^{(2}}{4}}={\frac {1}{2}}$, joka on helpompi ymmärtää. Kaikki tulokset pitää supistaa niin, että luvut ovat mahdollisimman pieniä.

Yhteenlasku murto- ja sekaluvuilla

Yhteenlaskussa on tarkistettava, että murtoluvuilla on yhteiset nimittäjät ja sitten laskettava osoittajat yhteen. Esimerkkejä:

• ${\frac {2}{5}}+{\frac {1}{5}}={\frac {2+1}{5}}={\frac {3}{5}}$

• ${\frac {1}{2}}+{\frac {1}{4}}={\frac {^{2)}1}{2}}+{\frac {1}{4}}={\frac {2}{4}}+{\frac {1}{4}}={\frac {3}{4}}$

• ${\frac {1}{4}}+1{\frac {1}{4}}=1+{\frac {1+1}{4}}=1{\frac {2^{(2}}{4}}=1{\frac {1}{2}}$

Vähennyslasku

Vähennyslaskussa vähennetään osoittajat, kun nimittäjät ovat yhtä suuret.

• ${\frac {2}{5}}-{\frac {1}{5}}={\frac {2-1}{5}}={\frac {1}{5}}$

Kerto- ja jakolasku

Kokonaisluvuilla

Kokonaisluvuilla jakaessa tai kertoessa murtoluvun osoittaja (kertolaskussa) tai nimittäjä (jakolaskussa) kerrotaan kerrottavalla.

• $2\cdot {\frac {1}{4}}={\frac {2\cdot 1}{4}}={\frac {2^{(2}}{4}}={\frac {1}{2}}$

• ${\frac {1}{2}}/2={\frac {1}{2\cdot 2}}={\frac {1}{4}}$

Murtoluvuilla

Murtolukuja kerrottaessa kerrotaan molempien lukujen osoittajat ja nimittäjät keskenään.

${\frac {5}{6}}\cdot {\frac {4}{5}}={\frac {5\cdot 4}{6\cdot 5}}={\frac {20^{(10}}{30}}={\frac {2}{3}}$

Murtolukujen välisessä jakolaskussa osoittaja ja nimittäjä vaihtavat paikkaa, jonka jälkeen se lasketaan kertolaskuna. (Tämän voi laskea myös kertomalla ristiin.)

${\frac {5}{6}}/{\frac {4}{7}}={\frac {5}{6}}\cdot {\frac {7}{4}}={\frac {35}{24}}=1{\frac {9}{24}}$